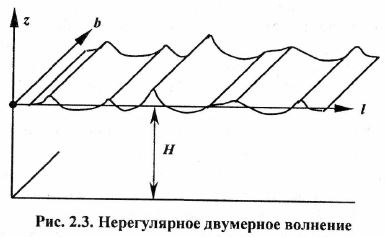
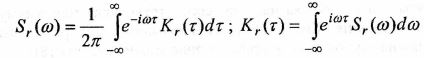В условиях волнения следующие одна за другой волны различаются между собой по амплитуде, периоду, длине, форме, протяженности гребней, направлению распространения. Волны, характеристики которых не повторяются, являются нерегулярными. Форма профиля реальных ветровых волн близка к трохоиде, но отличается от нее более крутым подветренным и пологим наветренным склоном. Напомним, что трохоидой называется кривая, описываемая точкой, лежащей на краю или внутри круга, который катится без скольжения по прямой линии. Нерегулярность и определенная хаотичность взволнованной поверхности моря дали основание рассматривать ее как случайное поле. При решении ряда задач волнение считают изотропным однородным случайным полем (рис. 2.3), представляемым совокупностью плоских нерегулярных волн со случайными фазами. В этом случае гребни волн имеют бесконечную длину, а профили индивидуальных волн во всех параллельных линии распространения вертикальных плоскостях – одинаковы.
Предположение об изотропности волн сводит трехмерное волнение к двумерному виду. Двумерная модель нерегулярного волнения довольно широко применяется при расчетах мореходности судов. Это объясняется тем, что протяженность гребней ветровых волн в среднем в два-три раза превышает их длину. У волн зыби это отношение еще больше. Когда волнение существенно влияет на судно, гребни морских волн по длине обычно больше судна, что и позволяет приближенно считать волнение двумерным.
Изотропное нерегулярное волнение характеризуется своим сечением плоскостью, перпендикулярной гребням. Волновую ординату в точке пространства считают случайным стационарным процессом, удовлетворяющим условиям эргодичности. Вероятностные свойства нерегулярного двумерного волнения отражаются рядом показателей.
Распределение ординат и амплитуд волн. В данной точке моря волновая ордината является случайной непрерывной величиной. Такие величины полностью описываются функцией плотности распределения. На основе многочисленных экспериментальных данных установлено, что значения волновой ординаты подчиняются нормальному закону. Амплитуды и высоты волн следуют закону Релея.
Главные характеристики волнения. При решении многих практических вопросов нет надобности описывать волнение плотностью распределения. Достаточно бывает ограничиться численной характеристикой его направления и интенсивности.
Направление волнения. В отечественной практике судовождения и в ряде других стран основными являются показатели стороны волнения против бега волн: Aw или q. В других зарубежных странах ими считаются направления по бегу волн: Kw или qw, отличающиеся от первых на 180°. Поэтому,
используя различные средства для оценки мореходности, необходимо обращать внимание на вид применяемых в них характеристик направления волнения. Ниже при изложении материала используются направления волнения против бега волн (q и Aw).
Интенсивность волнения. Силу нерегулярного волнения характеризуют в баллах, средним квадратичным значением волновой ординаты, высотой волн трехпроцентной обеспеченности, высотой значительных волн. Обеспеченностью называется вероятность в процентах факта, что высота волн окажется больше заданной величины. В районах больших глубин обеспеченность определяется в соответствии с законом Релея.
Среднее квадратичное значение волновой ординаты σr представляет собой квадратный корень из дисперсии волнения, рассматриваемого как случайный стационарный процесс. Этот показатель называют также наивероятнейшей амплитудой волнения. Ее обеспеченность составляет 60,6%.
В отечественной практике, а также в России, стандартным показателем интенсивности волнения считается высота волн трехпроцентной обеспеченности – h3%. Под высотой волны 3%-ой обеспеченности понимают такую высоту, вероятность превышения которой составляет 3%. Иначе говоря, h3% – это значение, больше которого могут быть только высоты трех из 100 последовательных волн.
В большинстве государств за рубежом силу волнения характеризуют высотой значительных волн — h1/3. Высота
значительных волн определяется как средняя одной трети наиболее высоких (из всей совокупности) волн. Эта высота имеет повторяемость 13,5%. Высота значительных волн называется также средней высотой самых больших волн и характерной высотой волнения. Для расчета h 1/3 по скорости истинного ветра Va при установившемся волнении Международной конференцией опытовых бассейнов (ITTC -International Towing Tank Conference) рекомендуется выражение:
Высота волн с обеспеченностью 0,1% условно принимается за наибольшую возможную в данном месте моря при шторме определенной силы. Различают также среднюю высоту волн (h = 0,625/h1/3), которая имеет обеспеченность 45,6%. В ряде источников можно встретить высоты волн другой обеспеченности, чем рассмотрены выше, например: 1% 2% 5%, 10%, 20%.
Корреляционная Функция волнения. Для описания вероятностных свойств изменения волновой ординаты во времени используется корреляционная функция Кг(т). В простейшем случае ее представляют выражением.
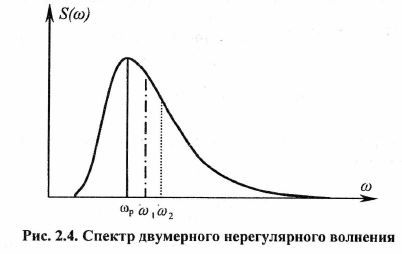
Здесь τ– разность моментов времени; σr – среднее квадратичное значение волновой ординаты; ωp – частота преобладающей гармоники волновой ординаты (гармоника, которая несет наибольшую энергию); cp – коэффициент затухания. Частота преобладающей гармоники волновой ординаты – это пиковая частота, соответствующая максимуму спектра волнения. Как показал Н.Н.Рахманин, для развитого волнения на глубокой воде приближенно можно считать.
Спектр волнения. По рассмотренным выше характеристикам морского волнения затруднительно находить показатели мореходности судна. Гораздо проще это выполняется при замене волновой ординаты как функции времени случайной функцией вспомогательной комплексной переменной, имеющей размерность частоты.
При переходе к частотной координате нерегулярное волнение рассматривается как результат наложения неограниченного числа плоских гармонических волн со случайными амплитудами, частотами и фазами. Для судна, принимаемого за линейную динамическую систему, это позволяет представлять его реакцию на морское волнение в виде суммы реакций на гармонические волны. В результате исследование влияния нерегулярного волнения на судно сводится к простым методам, которые применяются при изучении действия на него регулярного волнения.
Для частотной характеристики плоского нерегулярного волнения как случайного стационарного процесса используется функция спектральной плотности волновых ординат Sr (со) (энергетический спектр), представляющая распределение энергии волнения по различным частотам. Эту функцию также называют одномерным волновым спектром. Переход от временной к комплексно-частотной области с использованием спектральных характеристик позволяет значительно упростить выкладки при определении параметров качки по данным о волнении. Этот способ нашел широкое применение при расчетах мореходности.
Функцию спектральной плотности волновых ординат в общем случае можно представить графиком, изображенным на рис. 2.4. Гармонику, соответствующую максимуму спектра, называют преобладающей.
Спектр волнения связан с корреляционной функцией этого процесса выражением.
Как всякое распределение, спектральная плотность может быть охарактеризована интегральными параметрами моментами.
Спектральным моментом случайной функции со спектром Sr (ω) называется величина:
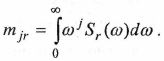Число j называется порядком момента. Оно может принимать любое целое положительное значение.
Через спектральные моменты выражаются характеристики, отражающие основные свойства волнения.
Дисперсия волновой ординаты. Момент нулевого порядка равен площади, ограниченной спектральной кривой. Он пропорционален полной энергии волнения и равен дисперсии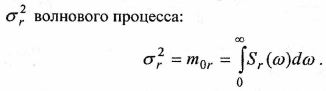 
Дисперсии скорости и ускорения волновой ординаты. Известно, когда случайный стационарный процесс имеет производную, то для получения ее частотного распределения
Идеализированные спектры морского волнения. Форма волнового спектра в данном месте и в данное время является неповторимой. Она зависит от текущих значений гидрометеорологических параметров, предыстории их изменения, географических и океанографических особенностей акватории. При практических расчетах, связанных с учетом волнения, для описания спектральной плотности волновых ординат используются предложенные рядом авторов функции. Они называются идеализированными волновыми спектрами, так как отражают только общие черты, присущие волнению всех морских глубоководных акваторий. По числу параметров, определяющих эти функции, спектры волнения бывают одно, двух и много параметрическими.
Для расчета спектров первого вида достаточно знать только один параметр – высоту волн. Для определения двухпараметрических спектров требуется знать высоту и средний период волнения. Из известных описаний распределения энергии ветрового волнения можно назвать спектры Ю.М.Крылова, А.И.Вознесенского-Ю.А.Нецветаева, Г.А.Фирсова, Пирсона-Московица, Неймана, Бретшнайдера, Хассельмана (спектр JONS W АР). Касаясь последнего распределения, следует отметить, что в 1968 и в 1969 году выполнялась обширная программа по измерению параметров ветрового волнения в Северном море, известная как JONSWAP (Joint North Sea Wave Project). На основе анализа ее результатов было получено выражение волнового спектра, названного по имени этой программы – JONSWAP. На 15-ой Международной конференции опытовых бассейнов (ITTC – International Towing Tank Conference) в 1978 году этот спектр был принят в качестве стандартного для Северного моря.
Большинство идеализированных спектров волнения относится к частотным распределениям, описываемых моделью:
где А, В,K,n– параметры, зависящие от статистических характеристик волнения и условий волнообразования.
Спектр смешанного волнения. Реальное волнение чаще всего является смешанным и состоит из ветровых волн и зыби. Энергетический спектр смешанного волнения существенно отличается от рассмотренных выше идеализированных частотных распределений ветровых волн. Он, как правило, имеет два максимума, которые приближенно соответствуют пикам спектров каждой из волновых систем, образующих смешанное волнение. Спектр зыби обычно расположен в области более низких частот, чем спектр ветровых волн. Для возможности учета особенностей двух систем волнения при решении практических задач Гидрометцентры в настоящее время передают прогнозы, как основных параметров смешанного волнения, так и его составляющих (ветрового волнения и зыби).
В современном программном обеспечении для расчета реакции судна на волнение используется обычно два волновых спектра – спектр ветрового волнения и спектр зыби. Реакция судна на смешанное волнение получается как сумма реакций на две составляющие его системы волн
