В теории управляемости приходится иметь дело с изучением движения судна на криволинейной траектории. При этом без существенных погрешностей, можно рассматривать движение судна в плоскости ватерлинии или параллельной ей плоскости. Таким образом, задачу определения элементов криволинейного движения судна можно рассматривать как плоскую задачу динамики.
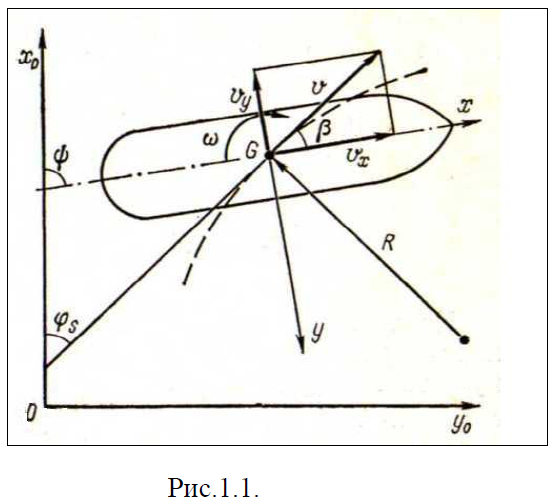
Для описания такого движения вводят две системы координат — неподвижную Х0О0 У0 , и подвижную ХGУ, жестко связанную с судном. Направление осей неподвижной системы координат выбирается таким образом, чтобы в начальный момент она совпадала с подвижной. Угол Ψ, образуемый с диаметральной плоскостью (ДП) и осью Х0, называется углом курса. Угол курса может быть выражен через другие углы, а именно через:
– центральный угол дрейфа, измеряемый между мгновенным. вектором скорости центра тяжести (ЦТ) судна и диаметральной плоскостью (β);
– угол траектории или угол скорости (φ) , измеряемый между вектором скорости и осью Х0.
Движение судна может быть задано проекциями скорости ЦТ на подвижные оси и угловой скоростью. Однако во многих случаях более удобной оказывается другая система кинематических параметров – модуль скорости ЦТ судна │V│, угол дрейфа (β), и угловая скорость (Ω). Обе системы кинематиче-ских параметров связаны между собой соотношениями, ясными из рис. 1.1
Все эти величины являются размерными кинематическими характеристиками, пригодными для описания любого вида маневра судна. Тем не менее, для сопоставления управляемости различных судов, и для пере-хода от модельных испытаний к натуре и т.п. более удобными оказываются безразмерные характеристики:
где V0 — скороcть судна на прямом курсе;
L- длина судна по действующей ватерлинии;
τ— безразмерное время.
Величина безразмерной угловой скорости является безразмерной кривизной траектории ЦТ судна: