Из рис.1.1 видно, что величины Ψ, β, φ связаны очевидным соотношением:
Дифференцируя соотношение (4) по времени, получим:
До сего времени речь шла о ЦТ судна, однако, все размерные и безразмерные характеристики могут быть определены для любой точки судна.
По известным формулам Эйлера, для точки «а» имеем:
Поскольку вектор угловой скорости имеет положительное направление, совпадающее с положительным направлением оси Ζ, для любой точки судна (i) можно записать:
Особый практический интерес представляет определение кинематических характеристик точек, лежащих на ДП судна. Для этих точек проекция угловой скорости на ось У равна 0 и можно записать:
Из формулы видно, что угол дрейфа уменьшается при перемещении в нос (βА0<βG) и возрастает при перемещении в корму от ЦТ судна (βА0>βG).
На ДП судна или её продолжении имеется замечательная точка, в которой угол дрейфа обращается в нуль, т.е. направление мгновенного вектора скорости будет совпадать с направлением оси Х, (или ДП). Такая точка называется цен-тром вращения судна (в некоторых источниках она называется кажущимся или мгновенным центром вращения, а также полюсом поворота), обозначаемым ЦВС. Абсциссу этой точки можно найти из выражения (9):
Из формулы (10) видно, что Хцвс всегда положительна. При малых углах перекладки руля, в случае движения судна по пологим траекториям Хцвс >L, а при больших углах перекладки — Хцвс = (0,35 + 0,60)L.
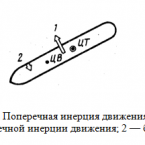
Ориентировочно можно считать Хцвс = 0,4L. Расстояние между ЦТ и ЦВ судна приближенно равно GC = RβG (рис.1.2)
При движении судна по криволинейной траектории проекция скорости на ось Х остается постоянной (VX= Const), а проекция на ось У будет увеличиваться по направлению к корме от ЦВС (рис. 1.2)
Если в результате натурного эксперимента или расчёта нам известны ки-нематические параметры криволинейного движения судна и их изменение во времени, то можно получить положение судна в плане на любой произвольный момент времени.
Координаты судна в неподвижной системе координат определяются следующими соотношениями:
Используя вышеприведенные соотношения можно построить траекторию движения ЦТ судна и определять направление его диаметральной плоскости.