Если при определении траектории движения спутника подразумевают его движение под действием только силы притяжения Земли, с одним притягивающим центром в центре масс Земли, то такое движение называют невозмущенным или кеплеровым. Если при определении траекторного движения спутника учитывают возмущающие силы, такие как притяжение Луны и Солнца, давление светового излучения, неравномерность гравитационного поля Земли и другие, то такое движение называется возмущенным.
Невозмущенное (кеплерово) орбитальное движение
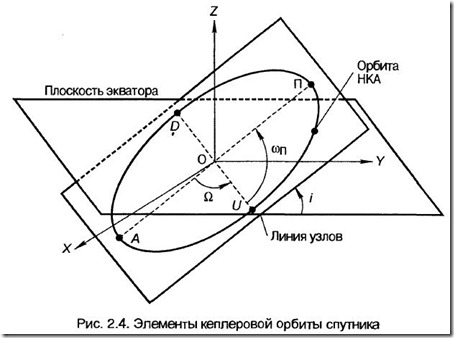
Первый закон Кеплера гласит, что любая траектория спутника, движущегося в центральном поле тяготения, лежит в неподвижной относительно инерциальной системы координат плоскости, проходящей через центр тяготения, и представляет собой кривую второго порядка, в одном из фокусов которой находится центр притяжения. Плоскость, в которой лежит траектория движения спутника, называется орбитальной плоскостью (рис. 2.4).
Проходящая через экватор плоскость XOY называется экваториальной плоскостью. Ориентация орбитальной плоскости характеризуется ее положением относительно экваториальной плоскости. Линия пересечения этих плоскостей называется линией узлов, а узлами орбиты спутника являются точки пересечения орбиты с экваториальной плоскостью. Узел U, образующийся при движении спутника из южной небесной полусферы в северную, называют восходящим, а узел D, образующийся при движении из северной небесной полусферы в южную – нисходящим.
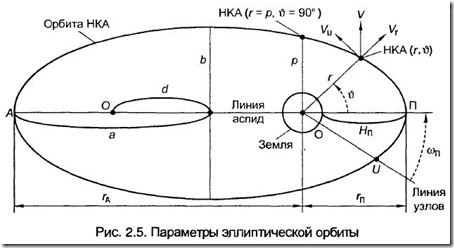
Эксцентриситет е определяет форму орбиты. При е = 0 орбита является круговой; при 0 < е < 1 эллиптической, с вытянутостью, зависящей от е и р; при е = 1 параболической; при е > 1 орбита имеет форму гиперболы. Навигационные спутники как правило движутся по эллиптическим орбитам, в одном из фокусов орбиты находится Земля.
Прямую линию, проходящую через фокусы эллипса О, называют линией апсид, а точки пересечения этой линии с эллипсом – апсидами. Ближайшую к центру полярной системы координат вершину (точка П) называют перицентром, а удаленную вершину (точка А) -апоцентром. Это обобщенные термины. Если спутник вращается по эллиптической орбите вокруг Земли, то эти точки называются соответственно перигей и апогей. Заметим, что точку апоцентра имеют только эллиптические орбиты.
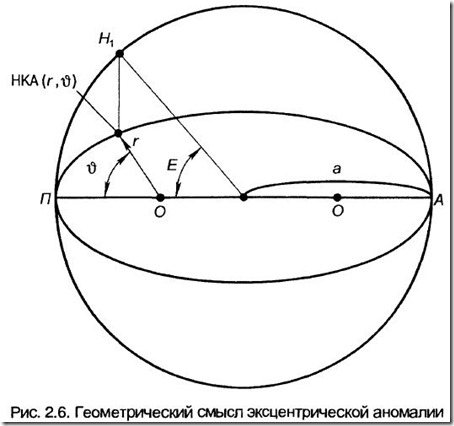
Геометрический смысл параметра Е проиллюстрирован на рис. 2.6, где кроме эллиптической орбиты спутника приведена гипотетическая круговая орбита. На ней фиксируется точка Н1, имеющая одинаковую со спутником абсциссу, и для этой точки определяется угловой параметр Е.
Когда спутник движется по эллиптической орбите, его угловая скорость непостоянна и зависит от положения на орбите. Для вычислений удобнее использовать равномерное движение с постоянной угловой скоростью. С этой целью вводится угловой параметр М – средняя аномалия для момента времени t, или средняя аномалия эпохи t: